매일 1문제 이상씩 풀기(2021 3/29~)
https://www.youtube.com/watch?v=kB93dyAL-GE
저작권 - 동영상 참조(안수빈님)
**시간복잡도(계산할 때는 최악의 상황을 고려해야 함)

O(1) : 1부터 N까지의 합을 구하시오, 단순한 수식으로 표현 가능
O(N) : 길이 N 수열에서 수 K 찾기, 최악의 경우 N번을 돌려봐야 함(확률적으로는 N/2번)
O(logN) : 정렬되어 있는 정보, 0~9에서 3을 찾는 과정, 계속 길이가 절반으로 줄어듬 => binarySearch

def binary_search(lst, N, K):
lo, hi = 0, N-1
while lo <= hi:
mid = (lo + hi) // 2
if lst[mid] == K: return True
if lst[mid] > K: hi = mid-1
else: lo = mid+1
return False
BigO notation은 점근적 표현법
시간과 공간차원에서 각각 다룰 수 있음 => 시간복잡도와 공간복잡도
계산 + 시스템에 대한 감(센스)이 중요

- 시간 제한과 메모리 제한을 확인하고 입력값의 범위를 확인한다.
1<=N<=100,000,000이면 O(N) 이상의 알고리즘(반복문)은 불가능
https://www.acmicpc.net/problem/1748
def solution(n):
ret = 0
for i in range(1, n+1):
ret += len(str(i))
return retdef solution(n):
return sum(map(lambda x: len(str(x)), range(1, n+1)))O(NlogN) : N은 반복문, logN은 str 연산
def num_len(n):
ret = 0
while n:
n /= 10
ret += 1
return retlog(10)N 의 연산으로 가능
2. 예제 입-출력 확인
예제 입력-출력은 보기 => 알고리즘화
def solution(n):
l, ret = len(str(n)), 0
for i in range(1, l): ret += i*(10**i - 10**(i-1))
ret += l*(n-10 ** (l-1)+1)
return ret
튜플로 기본 선언 시, 표현 간결
본인에게 익숙한 표현으로 변수 선언
코드 작성 완료
https://www.acmicpc.net/problem/2484
어떤 연산을 해도 1초가 안넘어간다
숫자가 같은지 안같은지 확인하는 가장 좋은 방법 = 정렬
def money():
lst = sorted(list(map(int, input().split())))
if len(set(lst)) == 1:
return lst[0] * 5000 + 50000
if len(set(lst)) == 2:
if lst[1] == lst[2]: return 10000 + lst[1] * 1000
return 2000 + (lst[1] + lst[2]) * 500
for i in range(3):
if lst[i] == lst[i+1]: return 1000 + lst[i] * 100
return lst[-1] * 100
N = int(input())
print(max(money() for i in range(N)))
**입력과 초기화 팁
num = int(input())
string = input()
char_list = list(input())
lst = list(map(int, input().split()))
map(x, y)는 x함수를 y의 원소에 모두 적용한 map 객체를 반환
나중에 char_lst 내용을 문자열로 만들고 싶다면? join 메서드
list초기화는 comprehension으로!
(1차원 배열)1st_1d = [0 for _ in range(N)]
(2차원 배열)1st_2d = [[0 for _ in range(N)] for j in range(N)]
**에러메시지

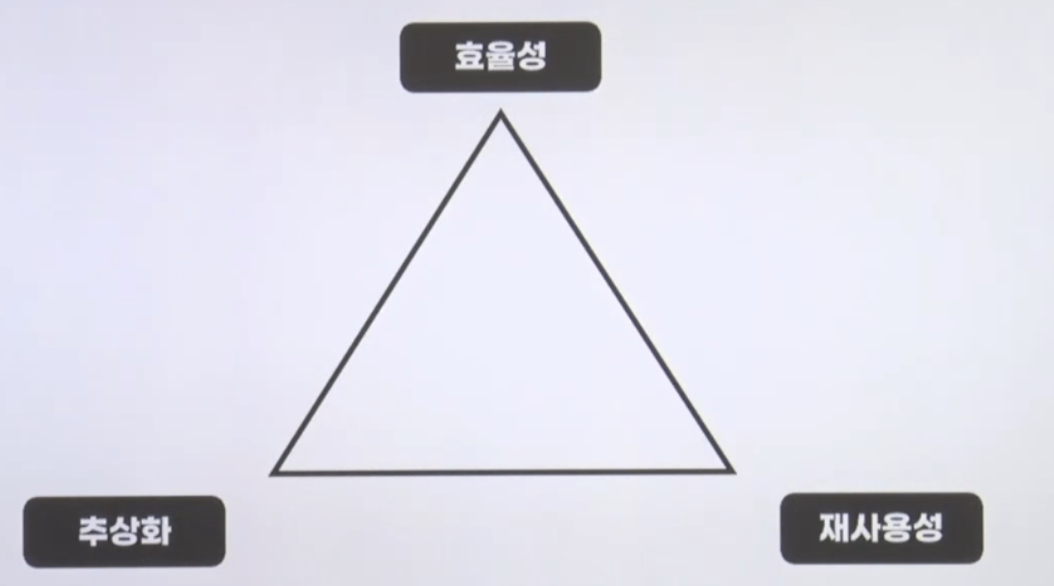
**추상화와 기능분리(함수의 활용)

=>기능 분리하기
https://www.acmicpc.net/problem/15684
(삼성 기출문제)

**가독성 : 조건문, 반복문, 함수 모두 줄일 부분 존재(indent 줄이기)


아래 코드와 같이 작성

else를 굳이 쓰지 않아도 리턴하면 함수 끝남
function2, 3번 쓰기
**명명법 : Snake, Camel, Pascal
snake_case, camelCase, PascalCase
--진수와 진법

어떤 수=>n진법

https://www.acmicpc.net/problem/1629
a**b%c하면 시간복잡도 O(b) = 시간초과
이진수를 활용하자!
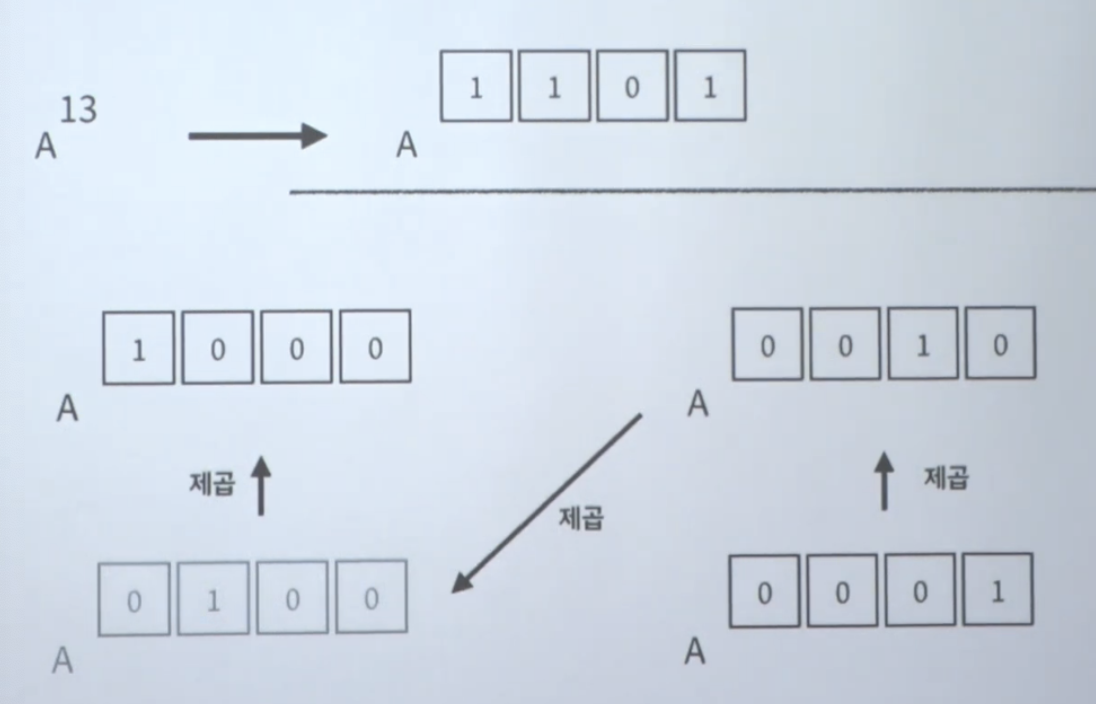


언제 mod를 씌울까?

중간중간에 나눠주는게 더 빠르다


아래가 더 빠름, min(ab)> o(1)
**유클리드 호제법
GCD(a,b) = GCD(b,a%b)
def gcd(a,b):
return b if a%b==0 else gcd(b, a%b)
--소수와 소인수분해

밑에 방법을 많이 사용
**에라토스테네스의 체


nlog(logn)
--분할정복(분해, 재귀함수)
**하노이탑
https://www.acmicpc.net/problem/11729

총 횟수 = n-1개를 두번움직이고 1일때는 하나이다

재귀함수 = 최저조건을 먼저쓰기
1,2,3번 기둥의 합 = 6
6-출발점-도착점 = mid
최소조건 = 탈출조건
--정렬(1,000,000*log100) = 20,000,000연산을 해라
- 선택정렬(selectionSort) : O(N^2)
- 버블정렬(bubbleSort) : O(N^2)
- 퀵정렬(quickSort) : O(Nlog(2)N), (⭐️면접단골질문)최악의 경우는 내림차순일 때 = O(N^2)
- 병합정렬(mergeSort) : 투포인터, 최악의 경우도 O(Nlog(2)N)라서 stable, 메모리가 넉넉할 때 사용
- 결국에 쓰는 정렬은 sorted => c언어 내부 정렬 알고리즘, 일정사이즈가 안되면 버블정렬, 일정수준이면 퀵, 병합으로 자동정렬
- radixSort : 최소값과 최대값의 범위가 작을 때
--자료구조 : 자료를 저장하는 방법론, 규칙
**stack = 괄호문제(push, pop)
FILO : First In, Last Out

https://www.acmicpc.net/problem/9012
괄호규칙
(())())
- )가 나오면 (랑 같이 지워주기
- ((((( -> len(stack)>0
https://www.acmicpc.net/problem/3986
https://www.acmicpc.net/problem/2504(조금 어려운 버전)
**Queue(task 분할 차원에서 많이 사용됨)
FIFO : First In, First Out

--stack & queue 쓰는 이유 : 메모리를 효율적으로 구현하기 위해서
**deque = stack + queue
https://www.acmicpc.net/problem/11866
요세푸스 = 수건돌리기 유형
리스트로 풀면 제거된 사람은 계속 거론되기 때문에 비효율적
from collections import deque
n, k = map(int, input().split())
dq = deque(range(1, n+1))
ans = list()
while len(dq):
dq.rotate(-k+1)
ans.append(dq.popleft())
print(f"<{str(ans)[1:-1]}>")
**Graph : 관계를 위한 자료구조
노드(Node)와 간선(Edge)으로 구성, 너와 나의 연결고리
들어오는 간선 수를 indegree, 나가는 간선 수를 outdegree
저장하는 방법 | 인접 행렬
- 방향성 추가
- 가중치 추가
https://www.acmicpc.net/problem/1389
ex)메이플 최단거리 => 다익스트라로 짬
Sparse한 그래프라면? 인접리스트

한붓그리기 = indegree가 짝수여야 한다
**Tree : 특수한 구조를 가진 그래프
그래프이기에 똑같이 노드(Node)와 간선(Edge)으로 구성
상위/하위 관계를 나눌 수 있음

부모(Parent)와 자식(Child)
선조(Ancestor)와 자손(Descendant)
뿌리(Root)와 잎(Leaf)

저장 방식은 자유롭게
부모만 저장 : 1개만 저장하면 됨
자식들저장 : root에서 뻗어나가기 쉬움
https://www.acmicpc.net/problem/2644
# 촌수계산의 핵심 = 공통된 조상찾기
# 공통조상으로부터 나와 그사람의 거리 = LCA
# n<=100이기 때문에 아무리많아도 O(n^2)
n = int(input())
a, b = map(int, input().split())
p = [0 for _ in range(n+1)]
for _ in range(int(input())):
x, y = map(int, input())
p[y] = x
aa, ba = [], [] # a의 조상, b의 조상
ad, bd = 0, 0 # 촌수
while p[a] > 0:
aa.append((a, ad))
ad += 1
a = p[a]
while p[b] > 0:
ba.append((b, bd))
bd += 1
b = p[b]
for i in aa:
for j in ba:
if i[0] == j[0]:
print(i[1] + j[1])
exit()
print(-1)
**Binary Tree : 신기한 특징을 가지고 있는 이진트리
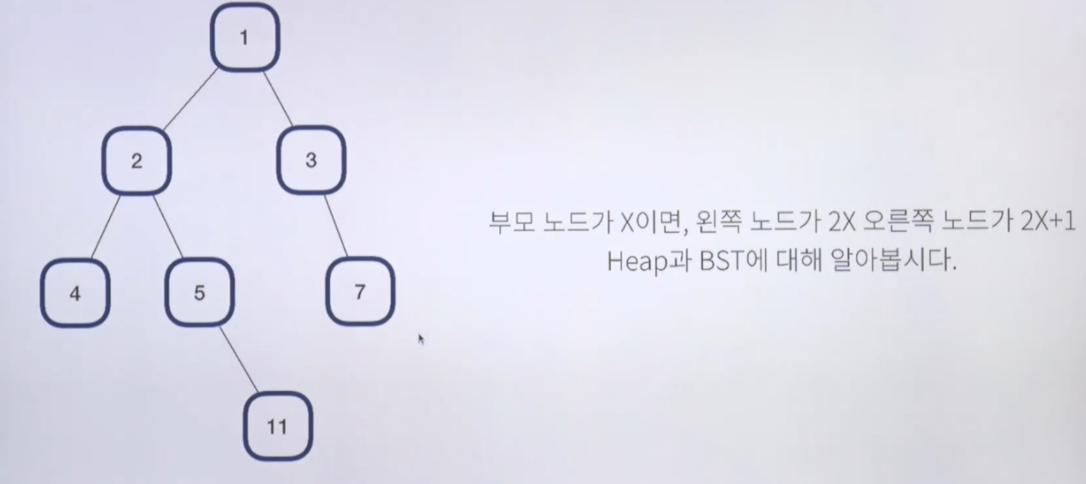
https://www.acmicpc.net/problem/13116
a = input()
b = input()
while not a==b:
if a>b: a //= 2
else: b //= 2
print(a)
**Heap : 우선순위가 가장 높은 값을 Root노드로 만드는 것 = O(logN)
HeapSort = O(NlogN)
**BST(Binary Search Tree) = O(log(2)N)
Balancing factor => AVL, Splan tree(bst를 회전해서 사용), 2-3-4 tree)
set, dict, hash를 이용해서 씀
--DFS & BFS
- DFS : Depth First Search 깊이 우선 탐색 (= stack과 유사)
-> 전수조사 Brute Force 완전탐색
주로 컴퓨터 메모리가 stack으로 재귀함수차원에서 관리
- BFS : Breadth First Search 너비 우선 탐색 (= queue와 유사)
-> 정답이 몇번 내에 나온다 하면 BFS사용
https://www.acmicpc.net/problem/2667
floodfill
# FloodFill = DFS
N = int(input())
A = [list(map(int, list(input()))) for _ in range(N)]
ck = [0 for _ in range(N)]
dx = [1, 0, -1, 0]
dy = [0, 1, 0, -1]
def dfs(i, j):
for way in range(4):
ii, jj = i + dx[way], j + dy[way]
if A[ii][jj] == 1:
dfs(ii, jj)
for i in range(N):
for j in range(N):
if A[i][j] == 1:
dfs(i, j)
https://www.acmicpc.net/problem/12851
# BFS
# 숨바꼭질 = 내위치, 동생의 위치
https://www.acmicpc.net/problem/16065
https://www.acmicpc.net/problem/1463
- 앞으로 공부하는 방법
https://www.notion.so/946e8b5351e1477fb351ab0fb2984154
개인이 생각하는 공부 유형 및 보완법
알고리즘을 공부하는 타입에는 다음과 같은 타입이 있습니다. 조금 전문적이지 못한 표현이 있을 수 있으나 이해를 위한 단어이므로 이해 부탁드립니다. 제가 본 몇 부류에 의하면 다음과 같이
www.notion.so
삼성 - DFS, BFS
카카오 - 트라이 자료구조
수비니움의 코딩일지 : https://youtube.com/수비니움의코딩일지
안수빈의 블로그 : https://subinium.github.io
A.I. Lookbook https://www.facebook.com/AI.Lookbook
알고리즘으로 고통받는 취준생을 위한 안내서 : https://www.facebook.com/algoguide/
삽질하는 디발자와 개자이너 : https://www.facebook.com/shovelingdesignoper